摘要:
借鉴了风格迁移的相关文献,提出了生成对抗网络的生成器架构,新的架构能够自动学习high-level 属性实现无监督分离和生成图像的随机变化,并且它能直观的再特定尺度上控制图像合成。新的生成器能获得更好的插值特性并且更好的解耦潜在因素的变化。提出了两种适用于任何生成器架构的新自动化方法。最后介绍了新的人脸数据集。
介绍:
生成式方法,尤其是生成对抗网络产生的图片在质量和分辨率上都得到了快速提升,然而生成器以黑箱方式运行,依旧缺乏可解释性,隐空间特性也很难被理解。
作者借鉴风格迁移的文献,重新设计生成器架构来控制图像合成过程,生成器从一个常量输入开始,在每个卷积层对图像的style进行调整,从而直接控制不同尺度下的图像特征强度。再向其中加入随机噪声,该架构变化能够导致high-level属性的自动,无监督变化,并实现直观的尺度混合和插值操作。对于鉴别器和损失函数不做其余修改。
生成器将输入嵌入到中间隐空间,对于变化在网络中的表征深远影响。输入潜在空间必须遵循训练数据的概率密度,我们认为这会导致某种程度的不可避免的纠缠。我们的中间隐空间避免了这种限制从而达到解耦。
最后,介绍了新的人脸数据集(Flickr-Faces-HQ, FFHQ),具有更高质量,覆盖更广的变化。
Style-based generator
首先看下Style-based generator 与传统架构的区别。
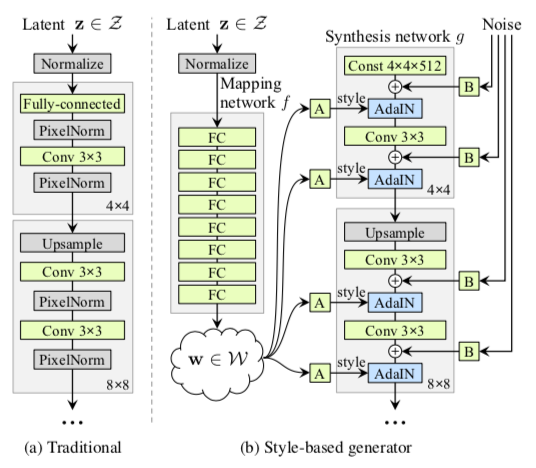
Mapping Netword
增加了一个Mapping network来对特征进行解耦,将input 映射到中间隐空间得到w。为输入向量z的特征解耦提供一条学习通道。
其结构图为:
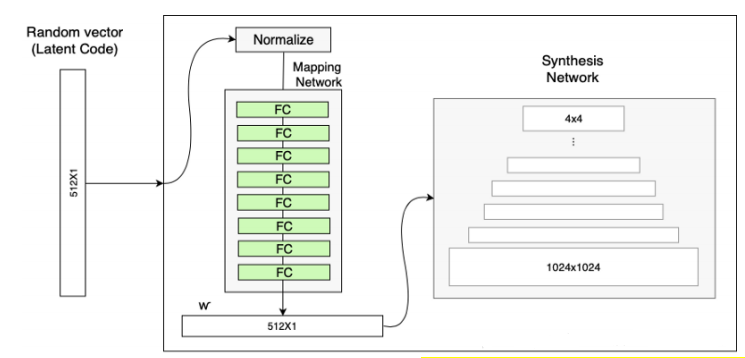
它由8个全连接层组成,同时输出向量w与输入向量z维度相同(512 $\times$ 1)。为什么使用一个MappingNet能实现解耦呢?
我们知道输入维度为512,但是512个维度并不能完整的表示面部所有特征,所以涉及到使用多个维度特征共同表示另外一个特征,Mapping Network的主要工作就是将它们解耦,使各个特征之间不存在相互影响。
首先是使用Mapping Network 将输入变换到中间隐空间中,经过A(仿射变换)从而获得18个512维度的不同style,用来单独控制生成图像的风格,网络通过这种方式自主学习如何将各个特征区分开来。
Synthesis Network(图像合成网络)
合成网络的输入为固定的(4,4,512)大小。其后由18层网络组成 18 = 1(初始输入的Conv层) + 16(8次 上采样和特征学习) + 1(最后一层转化为RGB的1$\times$1卷积)。经过8次上采样后特征图大小为(4->8->16->…->1024)。
该网络主要的输入包括style输入和noisy输入,分别用来控制图像的整体风格和细节。
style由仿射变换(A)产生缩放因子和偏移量($y_s, y_b$),使用AdaIN(adaptive instance normalization)对风格进行操作: \(AdaIN(x_i, y) = y_{s,i} \frac{x_i - u(x_i)}{\sigma(x_i)} + y_{b,i},\) 其主要功能是进行风格迁移。
noisy输入为高斯噪声组成的单通道图像,将其提供给合成网络的每一层。并使用单通道缩放因子将噪声图像广播到所有特征图。
具体网络细节等研究代码后在进行详细介绍。
Style mixing(风格混合)
使用两个随机潜码$z_1, z_2$得到中间潜码$w_1, w_2$使用这两个不同的潜码进行风格控制。具体做法是在图像合成中选定一个点,在该点之前使用$w_1$进行风格生成,在该点之后使用$w_2$进行风格生成。实验结果如下:

对于低分辨率($4^2-8^2$)的主要影响了high-level属性,包括姿势,发型风格,眼镜等。对于中分辨率($16^2-32^2$)主要影响具体发型以及眼睛是否张开等尺度风格。而对于高分辨率($64^2-1024^2$)主要影响色彩等细节信息。
Stochastic variation(细节变化)
对于细节主要包括具体的发丝,皱纹,雀斑等,这些细节并不会影响整体身份的变化。首先简要看下这些细节体现在哪些地方:

将噪声分别应用在不同的分辨率上以及不使用噪声来进行实验对比,实现结果如下:

其中(a)是在所有层均添加噪声后的效果。(b)是不添加噪声的效果,可见不添加噪声生成的图像一点也不个性化。(c)是只在高分辨率添加噪声,能够更精细的控制卷发,背景细节等。(d)是将噪声应用在低分辨率,对于发型的大曲度以及背景的整体进行改变。
总体来说,在所有层添加噪声,并不会影响到总体特征的变化,而只是在细节上进行改变,以生成具有不同个性的图像。
Truncation trick in $W$(对$W$进行截断)
考虑到训练数据的分布,对于低密度区域,生成器会很难学习到。因此采用截断的方式,来提高平均图像的质量,尽管这样做会丢失掉一些变化量。
具体策略是将那些偏离中心的特征距离进行收缩,但这并不会改变点与点的距离关系,将那些偏离中心过远的特征聚拢到一起,而不是单纯的丢到,因为不代表数据量少的特征不重要。其具体公式如下: \(w^, = \bar{w} + \psi(w-\bar{w})\)
$\psi$是一个实数,$w^,$表示截断后的值,后续的操作就使用改值来进行。对于$\psi$的作用,通过实验来说明:

当$\psi=1$是,表示没有进行截断的图,也就相当于原图,随着$\psi$减小,图像的的“个性”越来越小。当$\psi = 0$时,表示的是“平均脸”,随着$\psi$变为负数,可以看到图像的各个特征(比如脸的朝向,头发长度,性别等)都向着反方向变化。
解纠缠的研究
关于解纠缠的定义有许多,但是共同目标都是隐空间里的各个线性子空间能够单独控制一个因素的变化。$Z$一般需要符合训练数据集的密度分布,如下所示:
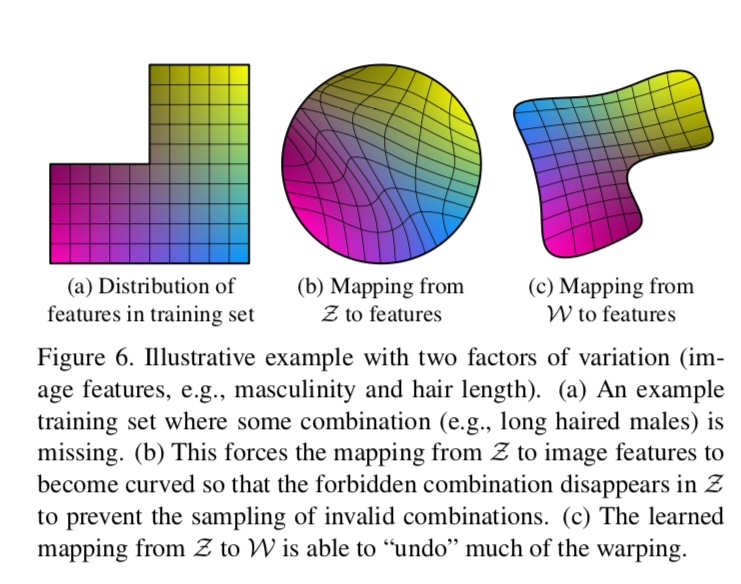
用两个变化因素(男子气概和头发长度)来说明纠缠问题。如(a)所示,训练集中缺少长头发且具有男子气概的分布,但并不代表真的不存在。(b)在隐代码$Z$中,它需要对特征进行弯曲以便覆盖确实的区域避免采样不允许的区域。(c)使用Mapping Network将$Z$ 映射到中间隐空间 $W$ 来“undo”这个过程。
这种方法之所以有效是因为生成器利用解耦的特征来生成图像要容易得多。然后具体提出了两个量化解纠缠效果的指标。
Perceptual path length(感知路径长度)
所谓感知路径长度是使用perceptual distance来进行计算,其计算过程是将两张待分析的图片送入VGG16网络中,得到各自的高级特征(因为对像素的差别我们不关心,而关系它总体来说特征是否相似)。利用高级特征来计算他们之间的距离。
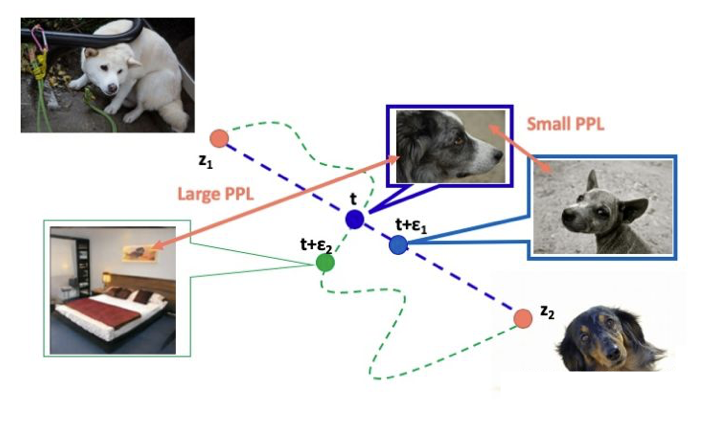
作者认为,如果一个隐空间的解耦效果好,那么,在这空间里的两个隐代码(latent code)$z_1,z_2$的变化路径长度应该更短(perceptual distance)更小。于是可以通过计算$z_1, z_2$和$w_1,w_2$各自之间的距离来判断解纠缠效果。计算公式如下:
\(l_Z = E[\frac{1}{\epsilon^2}d(G(slerp(z_1,z_2;t)),G(slerp(z_1,z_2;t+\epsilon)))],\) 其中$z_1, z_2\sim P(Z)$, $t \sim U(0,1)$,$G$ 表示生成器$g\cdot f$ $d(\cdot,\cdot)$ 表示perceptual distance。$slerp$表示球面插值。
对于$W$的感知距离计算如下: \(l_W =E[\frac{1}{\epsilon^2}d(g(lerp(z_1,z_2;t)),g(lerp(z_1,z_2;t+\epsilon)))],\) 由于$W$没有进行归一化,所以采用线性插值进行计算。实验结果如下:
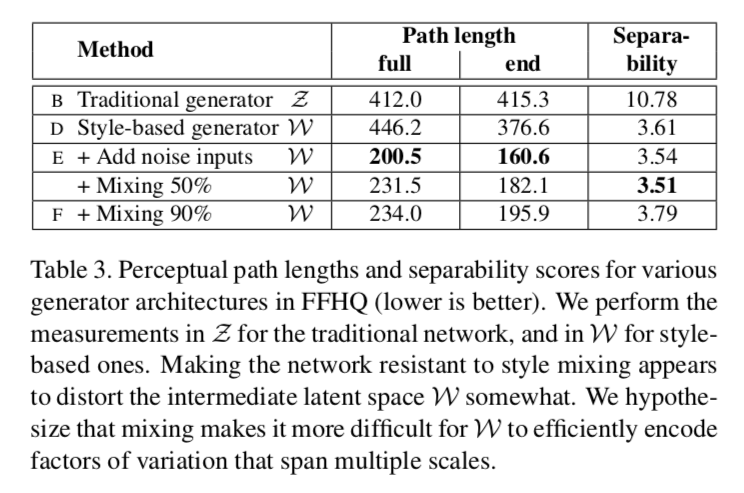
可以看出PPL确实减少了不少。
Linear separability(线性可分性)
这个观点非常直观,对于一些binary属性,作者认为不同属性的隐输入也是线性可分的。作者采用预训练的分类器将图片属性进行区分,然后再拟合一个线性分类器(SVM)将latent code分开。通过两个方式得到X-SVM预测的分类,Y-预训练分类器确定的类。使用conditional entropy $H(Y|X)$计算指标。对于所有的属性,使用 \(exp(\sum _iH(Y_i|X_i))\) 进行计算指标值。
结论
基于样式的生成器将传统的输入分离开来,使用Mapping Network将输入$Z$映射到中间隐空间$W$达到解纠缠效果。并将W输入到各个层中进行样式控制,使用AdaIN进行样式迁移。在合成网络中引入噪声来改变图像细节,而不改变图像全局样式。在对样式混合和细节控制以及中间隐空间的线性研究让我提高了对GAN的可解释性,并提高了可控性。最后提出了两个指标来对解纠缠效果进行量化。
在学习代码后将对具体细节进行补充,对错误的观点进行改正。后续将对StyleGAN更新版本进行阅读