Focal Loss

Focal Loss from kaiming

最初用于图像领域解决数据不平衡造成的模型性能问题

前言：

信息量

信息量是用来衡量一个事件的不确定性的；一个事件发生的概率越大，不确定性越小，则它所携带的信息量就越小。

假设X是一个离散型随机变量，其取值集合为$ X$，概率分布函数为$p(x)=Pr(X=x),x∈X$，我们定义事件$X=x_0$的信息量为： $I(x_0) = -log(p(x_0))$ 也就是说，当$P(x0)$越小，信息量越大
熵

熵是用来衡量一个系统的混乱程度的，代表一个系统中信息量的总和；信息量总和越大，表明这个系统不确定性就越大。

对于一个随机变量$X$，它所有可能取值的信息量的期望$E[I(x)]$就称为熵。 $X$的熵定义为： $H(X) = E_plog\frac{1}{p(x)} = - \sum_{x\in X}p(x)log\ p(x)$

条件熵

在随机变量$X$发生的前提下，随机变量$Y$发生所新带来的熵定义为Y的条件熵，用$H(Y X)$表示，用来衡量在已知随机变量$X$的条件下随机变量Y的不确定性。

\[H(Y|X)=H(X,Y)–H(X)\]

相对熵

相对熵(relative entropy)又称为KL散度(Kullback-Leibler divergence)，KL距离，是两个随机分布间距离的度量。记为$D_{KL}(p||q)$,它度量当真实分布为$p$时，假设分布$q$的无效性。

\[D_{KL}(p||q) = H_p(q)-H(p)\]

当$p=q$时,两者之间的相对熵$D_{KL}(p q)=0$

上式最后的$H_{p}(q)$表示在$p$分布下，使用$q$进行编码需要的bit数，而$H(p)$表示对真实分布p所需要的最小编码bit数。基于此，相对熵的意义就很明确了：$D_{KL}(p||q)$表示在真实分布为$p$的前提下，使用$q$分布进行编码相对于使用真实分布$p$进行编码（即最优编码）所多出来的bit数。
交叉熵

交叉熵描述了两个概率分布之间的距离，当交叉熵越小说明二者之间越接近

假设有两个分布$p$，$q$，它们在给定样本集上的交叉熵定义如下： $CEH(p, q) = E_p[-logq] = H(p)+D_{KL}(p||q)$ 当p已知时，可以把$H(p)$看做一个常数，此时交叉熵与KL距离在行为上是等价的，都反映了分布p，q的相似程度。

最小化交叉熵等于最小化KL距离。它们都将在p=q时取得最小值$H(p)$

交叉熵损失函数

Cross Entropy Loss的公式: $H_{y'}(y) := - \sum_{i}y_i'log(y_i)$ 其中$y_i$是预测结果，$y_i’$是GT

Q:为何不用 Mean Squared Error (平方和)

分类问题最后必须是 one hot 形式算出各 label 的概率，然后通过 argmax 选出最终的分类。

如果用 MSE 计算 loss，通过 Softmax后输出的曲线是波动的，有很多局部的极值点，即非凸优化问题 (non-convex)

样本不均衡问题

对于所有样本的均值函数为： $L = \frac{1}{N}\sum_{i=1}^{N}l(y_i, \hat{p_i})$ 直接考虑二分类问题，Loss： $L = \frac{1}{N}(\sum_{i=1}^{m}-log(\hat{p}) + \sum_{i=1}^{n}-log(1-\hat{p}))$ 其中m为正样本个数，n为负样本个数，N为样本总数，m+n=N

当样本分布失衡时，在损失函数L的分布也会发生倾斜，如m«n时，负样本就会在损失函数占据主导地位。由于损失函数的倾斜，模型训练过程中会倾向于样本多的类别，造成模型对少样本类别的性能较差

平衡交叉熵函数(balanced cross entropy)

解决样本不平衡问题，最直观的就是加上平衡因子

即： $L = \frac{1}{N}(\sum_{i=1}^{m}-\alpha log(\hat{p}) + \sum_{i=1}^{n}-(1 - \alpha)log(1-\hat{p}))$ 一般来说，$\alpha/(1-\alpha) = n / m$ ,就能改善正负样本不均衡问题

Focal Loss

focal loss也是针对样本不均衡问题，从loss角度提供的另外一种解决方法

focal loss具体形式如下： $L_{fl} = \left\{ \begin{aligned} & -(1 - \hat{p}log(\hat{p}))&if\ y=1 \\ &-\hat{p}^{\gamma}log(1-\hat{p})&if\ y=0 \end{aligned} \right.$ 为了将其表达为一种通用的表达，令: $p_t = \left\{ \begin{aligned} &\hat{p}&if\ y=1\\ &1-\hat{p}&otherwise \end{aligned} \right.$ 则$F_{fl} = - (1-p_t)^{\gamma}log(p_t)$

因此，$p_t$反映了与GT即类别y的接近程度，$p_t$越大说明越接近类别y，分类越准确。$\gamma > 0$为可调节因子

相比交叉熵损失，focal loss对于分类不准确的样本，损失没有改变，对于分类准确的样本，损失会变小。整体而言，相当于增加了分类不准确样本在损失函数中的权重。

$p_t$ 也反应了分类的难易程度， $p_t$越大，说明分类的置信度越高，代表样本越易分； $p_t$越小，分类的置信度越低，代表样本越难分。因此focal loss相当于增加了难分样本在损失函数的权重，使得损失函数倾向于难分的样本，有助于提高难分样本的准确度。focal loss与交叉熵的对比，可见下图：

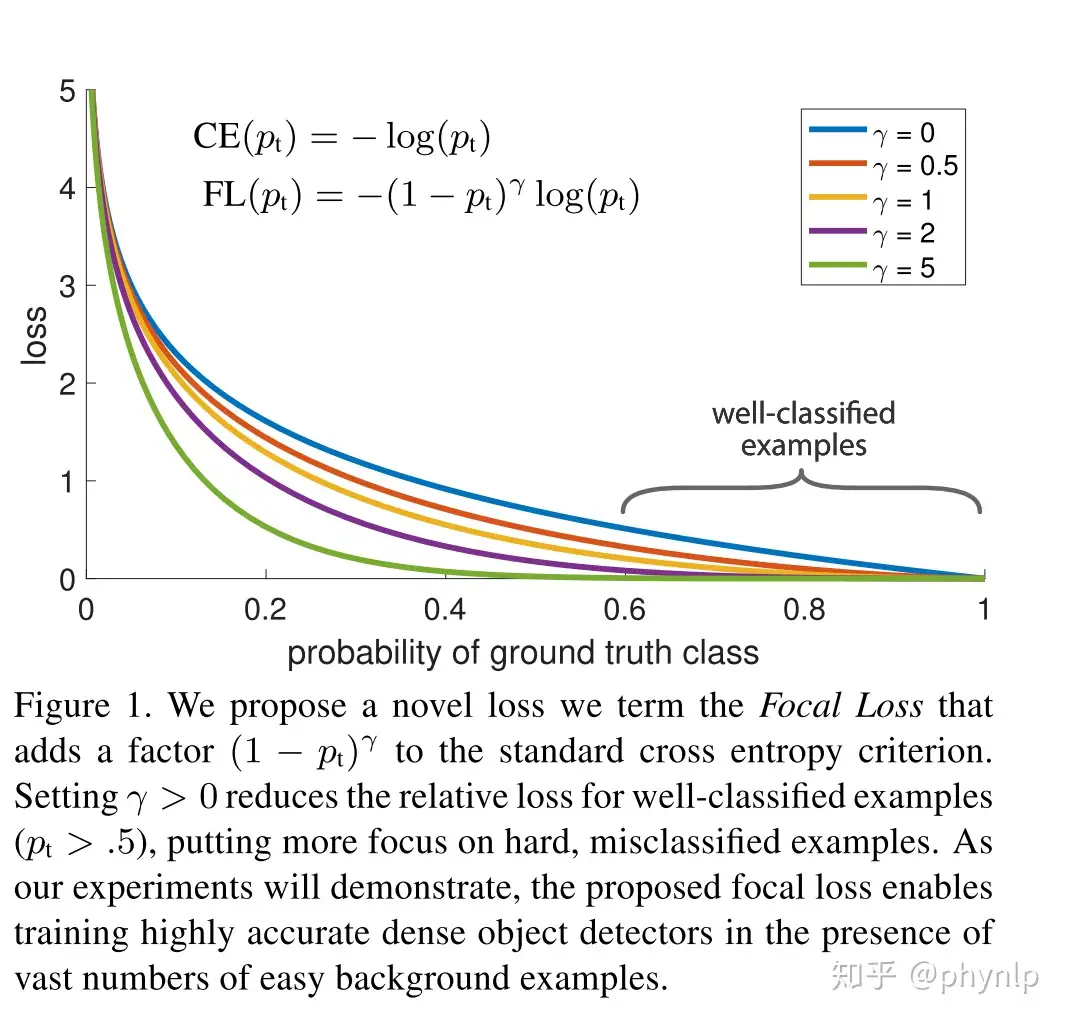
focal loss vs balanced cross entropy

focal loss相比balanced cross entropy而言，二者都是试图解决样本不平衡带来的模型训练问题，后者从样本分布角度对损失函数添加权重因子，前者从样本分类难易程度出发，使loss聚焦于难分样本。